椭圆焦点三角形面积公式
文章来源: 学好网
发布时间:2021-04-26 11:36
阅读:次
椭圆的焦点三角形是指以椭圆的两个焦点F1,F2与椭圆上任意一点P为顶点组成的三角形。焦点三角形面积公式是S=b2·tan(θ/2)(θ为焦点三角形的顶角)。

椭圆的焦点三角形是指以椭圆的两个焦点F1,F2与椭圆上任意一点P(不与焦点共线)为顶点组成的三角形。椭圆的焦点三角形性质为:
(1)|PF1|+|PF2|=2a
(2)4c2=|PF1|2+|PF2|2-2|PF1|·|PF2|·cosθ
(3)周长=2a+2c
(4)面积=S=b2·tan(θ/2)(∠F1PF2=θ)
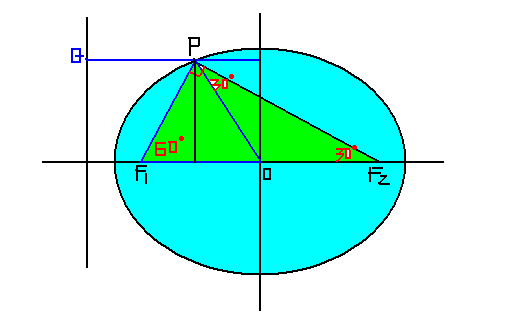
证明:
设P为椭圆上的任意一点P(不与焦点共线),
∠F2F1P=α ,∠F1F2P=β, ∠F1PF2=θ,
则有离心率e=sin(α+β) / (sinα+sinβ),
焦点三角形面积S=b2·tan(θ/2)。
已有
同学浏览观看
- 热门课程推荐 -








